In our technology-driven world, everything from smartphones and laptops to satellites and smart TVs operates on a language built not from words, but from just two symbols: 0 and 1. This language is known as the binary number system, and it’s the silent powerhouse behind every digital operation we rely on today.
Unlike the decimal system we use in daily life, which runs on ten digits (0 to 9), the binary system is based on only two digits. This simplicity isn’t a limitation; in fact, it’s what makes binary so powerful. Digital devices communicate, process data, and store information using a series of binary digits, or bits, where 0 represents OFF and 1 represents ON.
These two states align perfectly with the physical states of electronic components like transistors and logic gates. In this guide, we will break down the binary system in simple terms, explain how it works, and show you how to use it both manually and with the help of tools like a binary calculator.

What is the Binary Number System?
The binary number system is a method of representing numbers using only two symbols: 0 and 1. It is known as a base-2 numeral system, in contrast to the decimal (base-10) system most people use in everyday life. Each digit in a binary number is called a bit, short for binary digit. The position of each bit in the sequence determines its value based on powers of 2.
In this system:
- The rightmost bit represents 20=12^0 = 120=1,
- The next bit to the left represents 21=22^1 = 221=2,
- Then 22=42^2 = 422=4, and so on.
Example:
Let’s take the binary number 1011.
To convert it to decimal:
(1×23)+(0×22)+(1×21)+(1×20)=8+0+2+1=11(1 × 2^3) + (0 × 2^2) + (1 × 2^1) + (1 × 2^0) = 8 + 0 + 2 + 1 = 11(1×23)+(0×22)+(1×21)+(1×20)=8+0+2+1=11
So, 1011₂ = 11₁₀.
Binary Number Table:
The binary number table is a quick reference that shows how the first few decimal numbers (base-10) are represented in binary (base-2). This helps you visualize how numbers grow in binary and how each place value corresponds to a power of 2.
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
How Do We Count Using Binary?
Counting in the binary number system follows a pattern similar to decimal, but instead of rolling over at 9, it rolls over at 1 because binary only uses two digits: 0 and 1.
Binary Counting Steps: (H3)
- Start with 0 → 0
- Add 1 → 1
- Add 1 → rollover → 10 (like going from 9 to 10 in decimal)
- Continue adding 1 each time:
11 (3 in decimal)
100 (4 in decimal)
101, 110, 111, 1000, and so on.
Decimal vs Binary:
The decimal system (base-10) and the binary system (base-2) are both positional numeral systems, but they work with different sets of digits and base values.

Key Differences: (H3)
| Feature | Decimal (Base 10) | Binary (Base 2) |
| Digits Used | 0 to 9 | 0 and 1 |
| Base | 10 | 2 |
| Place Value Powers | Powers of 10 | Powers of 2 |
| Common Usage | Everyday math | Digital systems & computers |
Symmetry: (H3)
Binary numbers follow a very clean and symmetrical pattern. For instance:
- 1 in decimal is 1 in binary
- 3 in decimal is 11 in binary
- 7 is 111
- 15 is 1111
This symmetry happens because each of these decimal values is 2ⁿ 1, where n is the number of bits. It makes binary efficient for designing Binary Number systems where space and speed matter.
Binary Arithmetic Operations:
Just like in the decimal system, we can perform addition, subtraction, multiplication, and division in the binary number system. These operations follow basic rules adapted to only two digits,0 and 1.
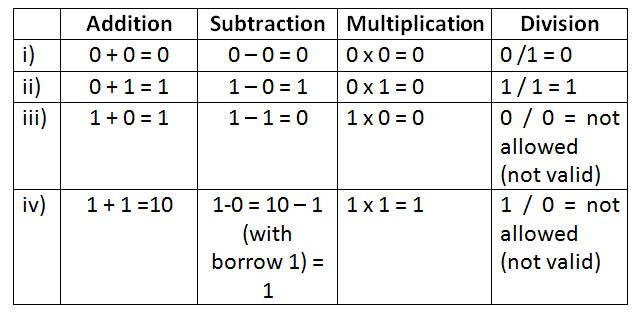
Binary Addition: (H3)
Binary addition is the most basic and widely used operation in computing Binary Number System(used even in CPU circuits).
Binary Addition Rules:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (0 with a carry of 1)
Example:
1011
+ 1101
——-
11000
Binary Subtraction:
Binary subtraction follows borrowing rules similar to decimal but adapted for 0s and 1s.
Binary Subtraction Rules:
- 0 − 0 = 0
- 1 − 0 = 1
- 1 − 1 = 0
- 0 − 1 = 1 (with borrow from next bit)
Example:
1101
− 1010
——-
0011
Binary Multiplication:
This works similarly to long multiplication in decimal, except we only multiply by 0 or 1.
Binary Multiplication Rules:
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
Example:
101
× 11
——-
101
+1010
——-
1111
Binary Division:
Binary division is like long division in base-10, but with simpler digits.
Binary Division Rules:
- 1 ÷ 1 = 1
- 0 ÷ 1 = 0
- 1 ÷ 0 = undefined
Example:
1010 ÷ 10 = 101 (which is 10 ÷ 2 = 5 in decimal)
Binary arithmetic is essential for everything from logic gates and circuit design to encryption and programming, and learning it opens up how computers “think” step-by-step.
Example of the Binary Number System:
Below are some direct and clear examples of how to convert binary numbers, including both whole numbers and fractional binary values, into their decimal equivalents. These step-by-step examples will help you understand how the binary number system works in practical terms.
Example: What is 1010₂ in Decimal?
To convert 1010₂ into decimal:
(1×23)+(0×22)+(1×21)+(0×20)=8+0+2+0=10(1 × 2^3) + (0 × 2^2) + (1 × 2^1) + (0 × 2^0) = 8 + 0 + 2 + 0 = 10(1×23)+(0×22)+(1×21)+(0×20)=8+0+2+0=10
Answer: 1010₂ = 10₁₀
Example: What is 1100₂ in Decimal?
To convert 1100₂ into decimal:
(1×23)+(1×22)+(0×21)+(0×20)=8+4+0+0=12(1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (0 × 2^0) = 8 + 4 + 0 + 0 = 12(1×23)+(1×22)+(0×21)+(0×20)=8+4+0+0=12
Answer: 1100₂ = 12₁₀
Example: What is 1.01₂ in Decimal?
To convert the binary fractional number 1.01₂ to decimal:
(1×20)+(0×2−1)+(1×2−2)=1+0+0.25=1.25(1 × 2^0) + (0 × 2^{-1}) + (1 × 2^{-2}) = 1 + 0 + 0.25 = 1.25(1×20)+(0×2−1)+(1×2−2)=1+0+0.25=1.25
Answer: 1.01₂ = 1.25₁₀
Example: What is 11.001₂ in Decimal?
(1×21)+(1×20)+(0×2−1)+(0×2−2)+(1×2−3)=2+1+0+0+0.125=3.125(1 × 2^1) + (1 × 2^0) + (0 × 2^{-1}) + (0 × 2^{-2}) + (1 × 2^{-3}) = 2 + 1 + 0 + 0 + 0.125 = 3.125(1×21)+(1×20)+(0×2−1)+(0×2−2)+(1×2−3)=2+1+0+0+0.125=3.125
Answer: 11.001₂ = 3.125₁₀
Converting Decimal to Binary:
Converting a decimal number (base-10) to binary (base-2) involves dividing the number by 2 and keeping track of the remainders. This method is widely used in digital systems and programming.
Steps to Convert:
- Divide the decimal number by 2.
- Record the remainder (0 or 1).
- Repeat the process with the quotient.
- When the quotient reaches 0, read the remainders in reverse order; this gives you the binary number.
Example:
Convert (25)₁₀ to binary:
25 ÷ 2 = 12 remainder 1
12 ÷ 2 = 6 remainder 0
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1
Binary result: 11001
(25)₁₀ = 11001₂
Patterns in Binary Numbers:
Binary numbers follow a simple but powerful pattern based on powers of 2. As binary digits increase, the value doubles with each additional bit.
Example Pattern:
- 1 in binary → 1
- 2 → 10
- 4 → 100
- 8 → 1000
- 16 → 10000
These numbers (1, 2, 4, 8, 16…) are powers of 2, and this pattern is the backbone of everything from memory addressing to file sizes in computing.
Uses of the Binary Number System:
The binary number system is essential in modern technology. Its simplicity makes it ideal for digital electronics and computing.
Common Uses:
- Computers: Every bit of data, text, image, and video is stored and processed in binary.
- Networking: IP addresses, subnetting, and protocols are built on binary logic.
- Digital Electronics: Binary signals control circuits, logic gates, memory, and processors.
- Programming: Low-level programming and bitwise operations use binary directly.
- Cryptography: Encryption and hashing algorithms rely on binary computations.
In short, binary is the universal language of machines.
Conclusion:
The binary number system may seem simple at first glance, using only 0s and 1s, but it’s the foundation of everything in the digital world. From computers and smartphones to software and networks, binary is how machines understand and process information.
By learning how to convert between binary and decimal, perform basic binary arithmetic, and recognize patterns in binary counting, you gain a deeper appreciation of how digital systems work. Whether you are a student, developer, or just curious, understanding binary helps you build stronger skills in computing and logic.
And whenever you need help with quick conversions or complex binary operations, don’t forget that a binary calculator can save time and ensure accuracy.
FAQs:
Why do computers use the binary number system?
Computers use binary because digital electronic components (like transistors) have only two stable states: ON (1) and OFF (0). Binary simplifies processing, storage, and logic operations in hardware.
What is the difference between binary and decimal systems?
The decimal system (base-10) uses digits from 0 to 9 and is used in daily life. The binary system (base-2) uses only 0 and 1 and is used by computers and digital systems.
What is a bit in the binary number system?
A bit (short for binary digit) is the smallest unit of data in computing and represents a single 0 or 1 in a binary number.
What is the 2’s complement method used for?
The 2’s complement is used to represent negative binary numbers and simplify binary subtraction in digital systems.
Is binary used in programming?
Yes, binary is used in low-level programming, and also in higher-level programming for bitwise operations and memory management.



